Armor penetration is a phenomenally complex issue, and one that isn’t wholly understood even today. But a basic explanation is necessary to understand why warship armor was designed the way it was during the dreadnought era.1 The basic factors that drive armor penetration can be roughly broken down into the armor, the shell, and how they meet. We’ll start with the last of these.

“How the armor and shell meet” boils down to impact velocity and obliquity, or angle of impact. A higher striking velocity is always going to result in higher penetration, all else equal. Obliquity is measured between the axis of the shell and the line normal (perpendicular) to the plate, so 0 obliquity is a direct hit and 80 degrees is a very glancing blow indeed. Oblique impacts have less penetration than direct ones, sometimes significantly so. This is not simply due to the geometry of the impact sending the shell through more metal, despite what most works that discuss armor penetration would have you believe. The front of the shell hits first, and the contact tends to make it rotate, either glancing off or hitting the armor side-first. This is obviously tremendously less efficient than a direct hit, and the usual counter was to design the projectile to dig in to the armor slightly, which would actually reverse this process. A shell hitting and piercing at high obliquity would come out with a lower obliquity than it went in at.2
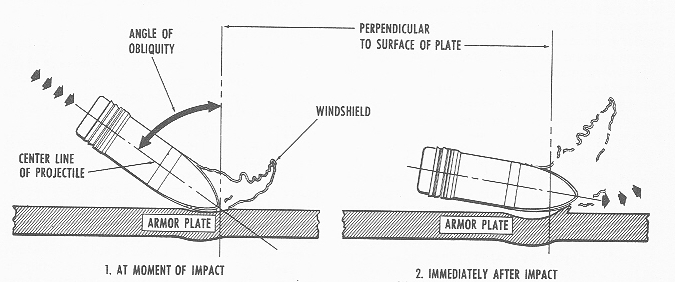
The effectiveness of the armor is a matter of thickness and material properties. Obviously, thicker armor is more difficult to penetrate, but at the same time, it’s heavier. The ideal material properties vary by application. For a battleship’s belt, the plates are usually decrementally hardened to approximately 30% of depth, and sometimes cemented. This hardened layer is intended to damage the projectile, making it less effective at piercing the rest of the plate, which is left soft and tough (resistant to cracking under sudden loading). Hardening armor makes it brittle, which can cause it to crack under impact. A fully-hardened plate is likely to simply crack at the point of contact and send a plug of armor flying into the interior of the ship, usually followed by the shell itself.
For thin armor plates, the most important factor is the thickness of the tough back, to the point where face-hardening armor under 3” or so actually makes it easier to penetrate. For deck armor, which is expected to be hit at very high obliquity, face-hardening is even worse. Besides the reduction in the tough back layer, the face-hardened layer significantly increases the chances of the shell breaking and digging in. The only use of horizontal face-hardened armor I’m aware of is on the tops of the turrets of the Richelieu class battleships, intended to counter bombing attack. Unfortunately, the only hit taken in this area was a battleship shell which penetrated, possibly due to the face-hardening.

The size of the shell is obviously important. The key metric is called sectional density, essentially the mass of the shell divided by the area of the shell. A heavier shell is going to perform better at a given impact velocity, but a gun of a given size is, to a first approximation, limited by energy, so a heavier shell will be fired slower. Overall, though, heavier shells tended to perform better, particularly as they carry more of their velocity to long range. The most famous example is the American superheavy shell. Shortly before WW2, the USN introduced longer, heavier versions of most of its shells. The pre-war 16" shell was 2100 lbs, while the final version was 2700 lb, and was considered equivalent to a conventional 18" shell at long range.
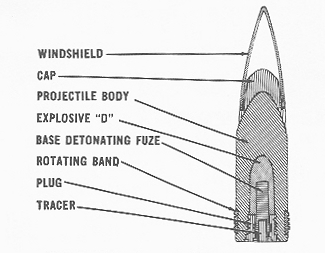
The design and construction of the shell is as important as weight. Armor works by breaking shells before they can penetrate, so a strong shell is obviously necessary. Face-hardening in particular was effective at shattering shells. Shell metallurgy evolved in parallel with armor metallurgy, with shells usually being forged and heat-treated. Face-hardening for a while shifted the balance in favor of armor, until the AP cap was invented.
The AP cap was more or less what it sounds like, a sacrificial cap on the AP shell designed to absorb the impact with the face-hardened layer and leave the shell intact to penetrate the armor. Initial caps were soft, but they were ineffective at high obliquity. Later hard caps were much less likely to be peeled off during impact, and remained effective at over 20° obliquity. They also acted as punch, creating a divot in the hardened face of the armor and helping the shell to dig in.
Another factor that could affect penetration was the shell's filling. A solid projectile, known as shot, is very good at penetrating armor, but it's also not particularly effective at doing damage behind it. An explosive filling is used to increase damage behind armor, but a poor choice of filling can render shells ineffective. The British used picric acid, which they called lyddite, throughout most of WWI. It was too sensitive, and had a bad tendency to detonate while penetrating the target's armor. Usually, a splinter layer behind the main armor would absorb the fragments produced. Many early fuzes had the same problem, detonating on impact or during penetration.

A dent in South Dakota's barbette from a 14" shell
Penetration was not an all-or-nothing phenomenon. Even armor that successfully kept out a shell might be dented, and it was not uncommon for a shell that didn't penetrate to throw fragments off the back of a plate (known as spall) or for some pieces of a broken shell to penetrate, while others were kept out. Depending on how the shell broke, it may or may not still have been able to explode.
This is just a brief overview of how the armor of battleships worked. There are lots of phenomena that I haven't covered, and the best place to start is with the information Nathan Okun has posted at Navweps.3
Next time, we'll look at the evolution of armor during the dreadnought era, including the rise of schemes optimized for long-range combat.
1 Before that era, armor schemes were relatively simple. ⇑
2 To put some numbers on this, I tried some experiments with Nathan Okun's FaceHard program. Pitting a plate at a 45 degree obliquity against a plate of 1.414 times the thickness at 0 degrees (so the plates themselves weigh the same for a given area protected), the sloped plate required the shell to be going 22% faster to penetrate. ⇑
3 Thanks to Nathan Okun for reviewing this post. ⇑

Comments
You don't f***ing say.
My department has a big display of chemicals that can be derived from coal. It's ancient, and has good-sized sample vials of all sorts of different derivatives. When an observant student noticed, and brought it to the attention of the department head, he did the rational thing and immediately closed down the department and called the bomb squad. Picric acid is firmly on my list of things I'll never work with.
@Eltargrim
I've heard several versions of that story before--not always picric acid, but the general idea of a chemistry department/lab having a 'collection' that, when noticed, requires a bomb squad.
Normally I'd say that indicates an urban legend, but the accounts tend to be first- rather than secondhand, so I think this might just happen a lot.
The problem is that the explosion would rather spend its energy pushing air than pushing steel. It follows the path of least resistance. There are ways to breach armor using explosives, but they weren't developed until WWII. Before that, you had to hit armor really hard to break it.
(Another disappearing post. I’ve asked Said Achmiz to look into this.)
Mind if I ask you a somewhat technical question about this?
When you write "The key metric is called sectional density, essentially the mass of the shell divided by the area of the shell" and "Shortly before WW2, the USN introduced longer, heavier versions of most of its shells. The pre-war 16″ shell was 2100 lbs, while the final version was 2700 lb, and was considered equivalent to a conventional 18″ shell at long range." It reminds me of this: https://en.wikipedia.org/wiki/Impact_depth Newton's approximation formula for impact depth. The depth of penetration is approximately the *length* of the projectile, multiplied by its relative density to what it's penetrating. Notably: -It does not depend at all on impact *velocity* or kinetic energy (although I think the formula assumes it's traveling at a high but not super-high speed. Maybe something in between Mach 1 and Mach 10). -It doesn't depend on the projectile *mass* but on it's length, because making the projectile wider would also mean an equal amount of extra armor to oppose it. -Increasing the projectile density does help, but assuming it's made of metal, it's hard to really increase density very much.
Does that sound about right? I realize this formula was only ever an approximation for a very complex subject, and it's just something Newton came up with in the days of cannonballs and earthen walls, but it seems to agree with a lot of what you're saying here and the design choices made.
More specifically, I'm thinking about the claims made here: https://navy-matters.blogspot.com/2022/10/missiles-versus-battleships.html that an anti-ship missile would not be able to penetrate battleship armor (or at least, that it's never been properly tested). My thinking is that, even though it's true that ASMs are not really designed to be armor piercing, they don't need to be, because they're so long. A harpoon missile is 15 feet long, plus it has the ability to hit dead-on rather than plunging at an oblique angle, so it would require something like 15 feet of armor to fully stop it. The 16" shells were only about 5 feet long in comparison. Maybe a bit better because of higher density, but not nearly enough to make up for the massive length difference. And the navy knows this, which is why they've never even bothered testing battleship-type armor against a modern missile.
That's my theory, anyway. What do you think?
That's only true at velocities high compared to the armor's strength, so likely valid against earth forts but not ships.
Also, a Harpoon isn't solid metal - while longer, it weighs less than a shell the same diameter.
The potential performance of missiles against armor is discussed here and here.
The Newtonian impact approximation is true for certain very specific cases, where the forces involved are high enough that basically everything can be treated as a liquid, but where there's not so much energy that you're just blowing everything up. (More specifically, at some point the energy-induced crater gets deeper than the Newtonian impact depth.) I forget the exact range, but it requires speeds well above what we see in combat today for the first assumption to start to hold. Note that Newton derived it on theoretical grounds, not based on seeing what would happen to a cannon fired at a stone wall, because it doesn't give a good result there.
The collision between a Harpoon and a battleship's armor is far too slow for anything like the Newtonian approximation to apply. Essentially, the Harpoon is a lot weaker than the battleship's armor, so most of the stuff you mention isn't really relevant. Only the warhead is even potentially strong enough to penetrate the belt. Everything else is just going to disintegrate on the armor, in much the same way that you'd expect to have really bad luck trying to pierce a steel plate by throwing plastic stuff at it. For that matter, there were essentially no cases in which a shell's sectional density wasn't much higher than the sectional density of the armor it was facing, and yet in lots of cases, the armor remained unpierced.
With regards to the wider point, I agree that existing anti-ship missiles wouldn't be able to penetrate a battleship's armor. But whoever wrote that post is wrong that you couldn't mission-kill a battleship with topside damage. That's a very real threat, and one that the battleships of olden times couldn't avoid, most prominently SoDak at Guadalcanal. I would also point out that developing a new warhead or even a new anti-ship missile is a lot cheaper than developing a new battleship. Oh, and torpedoes are also a thing.
Thanks for the link @muddywaters and detailed answer @bean. Sounds like that's not at all a good approximation, then. I was thinking it might work better at short range when the missile is still full of solid fuel, compared to long range when it's mostly empty. But it sounds like even that wouldn't be enough to matter, with the missile mostly doing damage from its warhead exploding rather than its momentum.