I've discussed the matter of battleship fire control at some length, but I focused on the various mechanisms necessary to compensate for the difficulty of shooting at moving targets at sea. What I didn't cover in any detail is the equally intricate process of making sure that the shell lands where you want it to 20 miles away.

USS Iowa firing a broadside
Let's start with the forces on the projectile. The most important is gravity. Obviously, gravity pulls the projectile down, and makes it curve. In a vacuum, it would form a perfect parabola, returning at the same angle it departed at, and falling at the muzzle velocity.
A quick examination of the range table for any naval gun will show that we aren't firing it in a vacuum. The next force to consider is that of drag. This is simple air resistance, slowing the projectile down along the line of flight. Drag reduces range and striking velocity, and makes the angle of impact steeper than the angle the projectile was fired at. This effect is larger for smaller shells. If we scale up a given shell shape, we discover that drag grows with the square of diameter, but weight grows with the cube, so the acceleration due to drag is inversely proportional to the size of the shell. Fire Control Fundamentals gives this example:
"Any projectile fired in a vacuum at an elevation of 40 degrees and with an I. V. of 2500 fps will attain a horizontal range of 192,000 yards (almost 100 miles). At the same elevation in air, a 16-inch projectile will attain a range of only 42,000 yards, a 5-inch projectile 17,000 yards and a 1.1-inch projectile only 7000 yards."
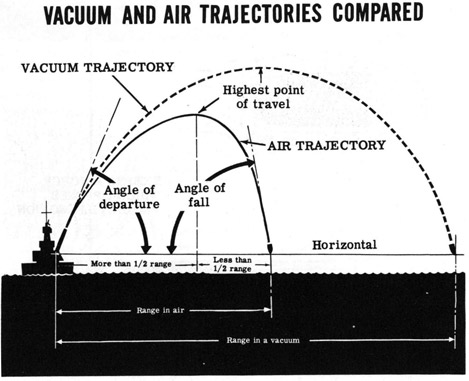
The other factors are projectile velocity, air density and shape. Long, pointed shells are less draggy than blunt ones, and many AP shells had long ballistic windscreens to improve range, as the form required for armor penetration was fairly blunt.1 Drag is proportional to the square of projectile velocity, resulting in quick dropoff in velocity, and also proportional to air density. This could be significant on the scales involved. The USN range table2 for the 16"/50 gives a maximum height of 36,600 ft for a round fired at 45° (range 42,345 yds), at which altitude the air is only about 30% of its sea-level density. This may be why the striking velocity actually reaches a nadir at 34,000 yds, increasing 8% above that value at maximum range.3

USS Missouri, with shells in flight circled
The obvious question at this point is how the projectile stays stable, as flying through the air sideways would tend to increase drag, as well as making the point of impact rather unpredictable. The answer is rifling, a series of spiral grooves4 cut in the barrel and engaged by a soft driving band on the projectile. This imparts a stabilizing spin to the projectile. The usual example given is how an American football is made to spin, but some of you may not be familiar with that.5
The spin holds the projectile in a stable orientation, much like a top. However, the stable orientation is that of the muzzle, and thus as the shell's trajectory drops, the air is coming from slightly below the nose of the shell. This should push the nose of the shell upward, but because the shell is a gyroscope (and therefore magic), it instead precesses to one side. All naval guns used a right-hand twist, and thus tended to point their noses to the right of the course. This pushes the shell off to the right. This effect is barely noticeable at short ranges, but could be as much as 1,850 yds for a 16" shell at maximum range.6
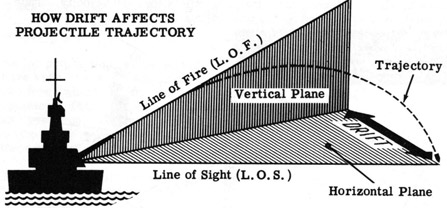
Gravity, drag, and drift are the basic forces accounted for on range tables, but they are far from the only factors that affect where the shell lands. The USN divided these into two groups: Group A, which are independent of target bearing, and Group B, which are dependent on target bearing.
Group A errors are variations in muzzle velocity due to either powder temperature or barrel erosion, and variations in drag due to air density. A 1°F change in powder temperature would produce a 2 ft/s change in MV. At 40,000 yds for a 16" AP shell, that could translate into a 55 yd change in the point of impact. As rounds are fired through them, barrels wear out, and the shell fits less tightly, decreasing muzzle velocity. A new 16"/50 Mk 7 would generally produce a muzzle velocity (AP shell) of 2500 ft/s, falling to 2425 ft/s for an average gun. This costs 2,160 yds of maximum range, and more if the gun is badly worn.7
A complicated nomogram was provided in the range tables for air density corrections. I don't have a 16" gun sheet, but I do have one for the 5"/38. At 15,000 yards, going from the standard conditions on the chart to a hot day in the South Pacific might result in a range error of 300 yds long, while the North Atlantic in winter would be short 360 yds at the same barometric pressure.
Group B errors are from wind, and motion of the target and the gun. Target motion correction was adequately covered in my posts on fire control, although it bears emphasizing that a target moving at 30 kts covers over 1,500 yds in the time it takes a 16" shell to reach maximum range. Wind is broken down into range wind, along the line of sight, and cross-wind, perpendicular to the LoS.
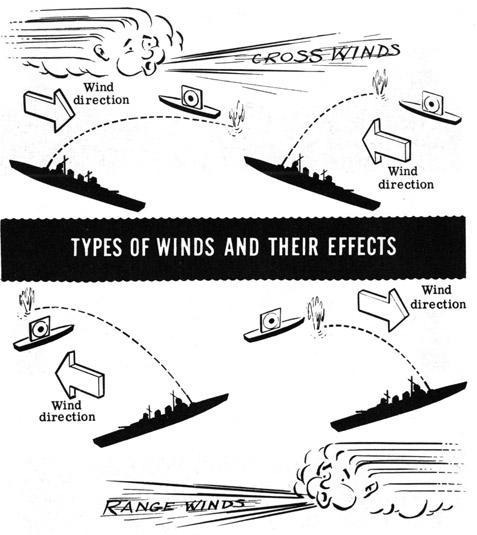
For our typical example, a 10 kt range wind would result in a 200 yd deviation, while a 10 kt cross-wind would push the shell 126 yds off target. Wind is made even more complicated to compensate for because it isn't necessarily continuous throughout the projectile's flight. The wind at 30,000 ft isn't necessarily the same as at sea level, and the values on the range table assume constant wind. There's no good way to deal with this problem, except through spotting, which makes long-range gunnery all the more impressive.
The motion imparted to the projectile by the ship has two effects. It changes the initial velocity of the shell, but also creates a 'virtual wind' which slows the shell down relative to this initial velocity. In a vacuum, if two ships were steaming along on parallel courses and at the same speed, there would be no need to compensate for either motion, as the movement of the target would be countered out by the change in shell velocity. In practice, this is modeled as assigning all velocity to the target, and adding in extra wind equivalent to the firing ship's motion.
Knowing about what makes a projectile land where it does isn't a complete solution to the gunnery problem. The range table is slow and awkward to use, and mechanical methods of compensating for these effects were soon devised.
2 I ended up using a mix of OP 1188 and OP 1457. OP 1188 is the summary table, and has data for many guns, including the AP shell at 2500 ft/s. However, it does not have the correction values for velocity errors and wind, so I was forced to use OP 1457, which does have those values, but has the data for the AP shell at 2425 ft/s instead. ⇑
3 I believe this is caused by the dramatic climb in maximum altitude/elevation angle with range. At 22,000 yds, the gun is elevated 13° 23.5', with a maximum altitude of only 4,470 ft. The velocity nadir is at an elevation of 26°, and the peak altitude is 14,730 ft. ⇑
4 Iowa's guns have 96 ⇑
5 Don't worry. It's no real loss. ⇑
6 This is another value which increases greatly near maximum range. It's 949 yds at 36,000 yds. ⇑
7 The 16"/50 Mk 7 had a 290-equivalent service round (ESR, AP shell at full charge) barrel life when initially introduced, raised to 350 ESR by the Korean War. Various additives had raised this fourfold by Vietnam, and by the 1980s, wear was so low that the guns were limited by fatigue life, to about 1,500 Fatigue Equivalent Rounds each. HC shells at full charge were initially .43 ESR, while target rounds were less. Ships usually had their barrels replaced when remaining life was equal to the per-gun ammo load, ~135 rounds for the Iowa. I don't have the round-by-round erosion data for the Mk 7, but I do know that Iowa herself was only regunned once, after firing a total of 8,279 rounds (average of 920 per barrel), most of which were HC. ⇑

Comments
As I understand it, some land-based artillery would get greater range by firing at higher than 45 degree angles, getting a bigger gain from less air resistance at high altitude than they lost from the high angle. Though presumably it would have been basically impossible for a ship to hit another ship with that strategy (with such extreme range and even longer flight times for the projectile), it seems like it might have been useful at times for shore bombardment to be able to do it from further away or hit targets further inland. But it seems none of the big naval guns were capable of being elevated even to 45 degrees, never mind higher yet. Was it that hard to make the guns capable of greater elevation?
The Iowa's guns did elevate to 45 deg. 15 was pretty typical in WWI, and 30 was standard for interwar reconstructions. The big problem with high elevation in naval guns is that it complicates the mountings. I suspect that heavy naval guns get their shells high enough that elevations much above 45 deg aren't particularly helpful. Also, shore bombardment was never a major design driver.
How much does the firing angle affect the ship from which it is being fired? High angles should pretty much push it down which I guess is a non-issue, while shallow angles might tend to flip it (especially if ballast is low).
Or is energy in projectiles just too small relative to mass of the ship?
There's not enough momentum in the projectiles. For Iowa, a full broadside at 0 elevation would get you going about 6 in/sec totally disregarding any forces stopping the ship. A lot of former crew swear the ship moves, but it's not true. And pictures that look like the ship moving sideways are the muzzle blast interacting with the disturbed water from the ship's movement.
Right, except forces stopping the ship are down below the water, and forces pushing the ship are up above the water, which makes perfect rotational couple and which tends to flip the ship over. And 6 in / sec is faster than a human walking, so I would expect it at least to bend.
Obviously ships don't flip over when firing. And not so obviously sailboats (where sail is kind of like gun firing) do flip sometimes. So I wonder if there is something else to help here, ballast or guns venting gasses back or springs or something.
First, 6 in/sec is slower than a human walking by close to an order of magnitude.
I'm having a little bit of trouble directly quantifying how fast the ship would rotate in free space, so let's look at your other example, sailing ships. Yes, most of their motion is forward, but they do make leeway, so we know they're moving sideways. And they have to keep from flipping over. I'm pretty sure that 6 in/sec (.3 kts) is a fairly small amount of leeway by normal standards. And Warrior (to grab the first example to hand) has a metacentric height (the measure of stability) half that of Iowa. And the center of effort of the guns is a lot closer to the center of mass than the center of effort of the sails. The ship may rock a bit, but from what I've heard, that's not even really true.
Yup you are correct about speed. I moved decimal point to the left accidentally while recalculating speeds. Combined with shorter center of effort it should be nigh impossible to flip it over.
It happens to all of us. I do think you're right in that I'd be fairly worried about the ship going over if it was moving sideways at all, but the ship is very heavy in comparison to the shells. If it rolled appreciably, I think they'd be a lot more careful about making sure the turrets were synchronized when firing, and they weren't.
Question about the gyroscopic stabilization you talk about: you seem to be implying the shell (mostly) stays at the same inclination as when it's fired through the whole trajectory -- nose up.
I thought that AP shells relied on hitting nose-first. Can you say more about what goes on here?
This is something I'm still kind of confused about myself. The shell wants to retain the orientation it came out of the barrel at, and so it flies a bit nose-up. This leads to drift. However, the angle of attack never gets too big (can't say exactly how big offhand, sorry), so the shell does strike pretty much nose-on. I'm not sure of the exact mechanism that makes the shell turn to follow the line of flight. I looked, and couldn't find anyone who could say. I may do more research on this.
@Andrew I've looked into this more, and I'm still confused. The best explanation I have is that the shell precesses to the right, which means that you also have air striking off-center and pushing it to the right. That force in turn makes it precess down. What I don't understand is how the magnitudes work. The precession to the right should be significantly greater than the precession down, but a shell can turn 90 deg in flight, while drift isn't nearly that much. I'd like to know what's actually going on, but I'm not sure where to look. Edit: Several sources confirm this mechanism. I'm surprised it works, but it definitely seems to.
On the gyroscopic orientation question, I suspect the correct answer lies in the aerodynamic moment being generated by the lifting body being balanced with the restorative torque of a gyroscope. The angle of attack is self limiting to a small value above the flight path as the gyroscopic restoring torque must always balance out the applied load (in a stable flight path admittedly). The angle of attack is probably set by the rotation speed so I suspect if you really cared about keeping the AOA small, you would put canted fins or something else on the shell to improve the pointing accuracy of the nose. This all happens independent of the force balance on the part, so bean's description of the flight path mechanism can be thought of as a separate if related process. Interestingly enough, the pointing accuracy increases with shell speed (or Air density). Similar behavior drives spin stabilized solid rockets, which typically have spin motors to get them spinning as fast as possible when they are still at low speed coming of their launch rails to keep them from drifting into your ground infrastructure, although the concern is a little worse there, since the propulsive force can act to drive an unstable aerodynamic spin, also know as the "oh shit, hit the deck moment"
Caption currently reads “boradside”
Oops. Well, that typo survived for over four years.
Possible spam comment above.
I guess no place is safe from this kind of moronic spam stuff.
Comments are locked due to persistent spam. If you have something to say, feel free to use the OT.