When I first talked about fire control, I briefly mentioned the problems of rangekeeping. This is the practice of turning the ranges produced by rangefinders into values that can be used for gunnery. I'll expand on them, and look at the early mechanisms used to solve these problems.
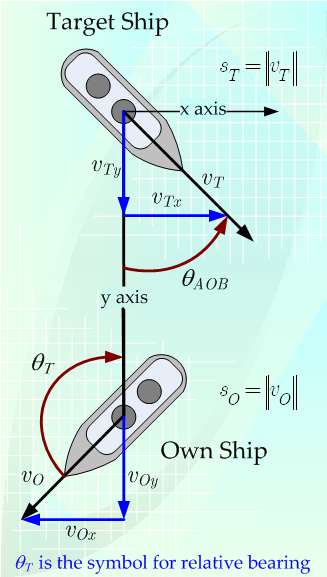
The first problem is that rangefinders do not produce the ranges that the guns need to be aimed at. A good rangefinder will produce a close approximation of the current (geometric) range to the target,1 and this is adequate at short ranges. As range increases, the shell falls more steeply, which decreases the "danger space", where the shell falling long or short will still hit. Even worse, long-range fire takes longer to reach the target. Even if rangefinder range is accurate and can be transmitted instantly to the guns, the target will have moved by the time the shells reach it. The obvious solution is to predict where the target will be, and to aim there, but this is harder than it looks, because both the ship and the target are moving, and the solution changes as the ships move. Solving any specific case might not be that difficult on paper, but solving the problem in real time is a very different matter.

John Dumaresq
In 1902, Lieutenant John Dumaresq realized that this problem was solvable. The velocity vectors of the two ships were independent of their relative positions, and could be added up to produce a single relative velocity vector. If this was assigned to the target ship, it could easily be broken down into speed along the line of sight, also known as range rate, and speed across the line of sight.2 Speed across was often divided by the range to the target to get bearing rate, which was much easier to deal with when setting gunsights. Dumaresq spent the next two years developing this concept into a mechanical slide-rule that bore his name. The Dumaresq had a large bar for the ownship course and speed, a smaller pointer mounted on it for the target ship,3 and a rotating scale for the line of sight, which allowed the operator to quickly generate a solution for range rate and rate across. Another interesting feature of the Dumaresq, and of side-rules in general, is that they represent a coherent solution, and don't care what you use as the input and output variables. For instance, if range rate and rate across are known, it's trivial for the operator to take a "cross-cut" and work out target course and speed.
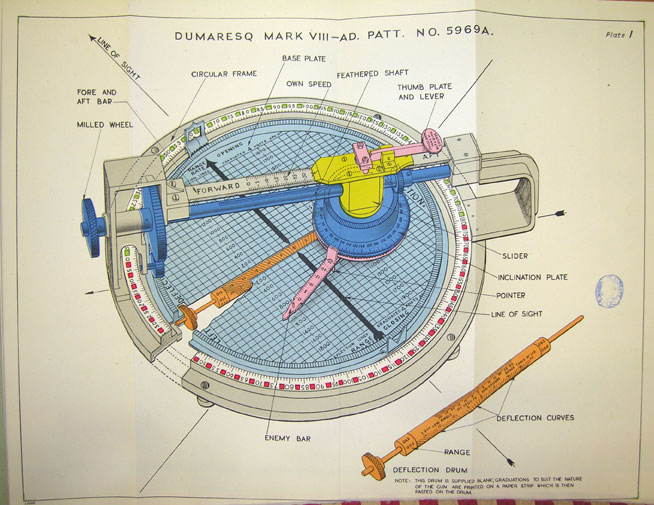
A Dumaresq
The Dumaresq was an example of what is known as the "synthetic" solution to rangekeeping. This meant that a solution was estimated and then checked against reports coming in. The alternative was known as the analytic method, which attempted to derive range rate and possibly bearing rate from directly-observed data. For instance, a simple plot of how quickly rangefinder ranges change with time could have a line drawn through it, and the slope plotted. When this system was plotted head-to-head against the Dumaresq, it was discovered that the synthetic system was significantly better, due to the scatter in rangefinder ranges, which might be several hundred yards at the distances expected in battle.

Admiral Sir Percy Scott
But finding the range rate was only a partial solution to the problem of rangekeeping. A typical rangefinder might be able to take four ranges a minute, and in battle, it would not be unusual for this to fall even farther, while the true range changed. As such, a device was needed to keep track of the present range, and then-Captain Percy Scott, the RN's leading expert in long-range gunnery, provided it. The so-called Vickers Clock, named after its manufacturer, quickly became the standard instrument for naval fire-control.
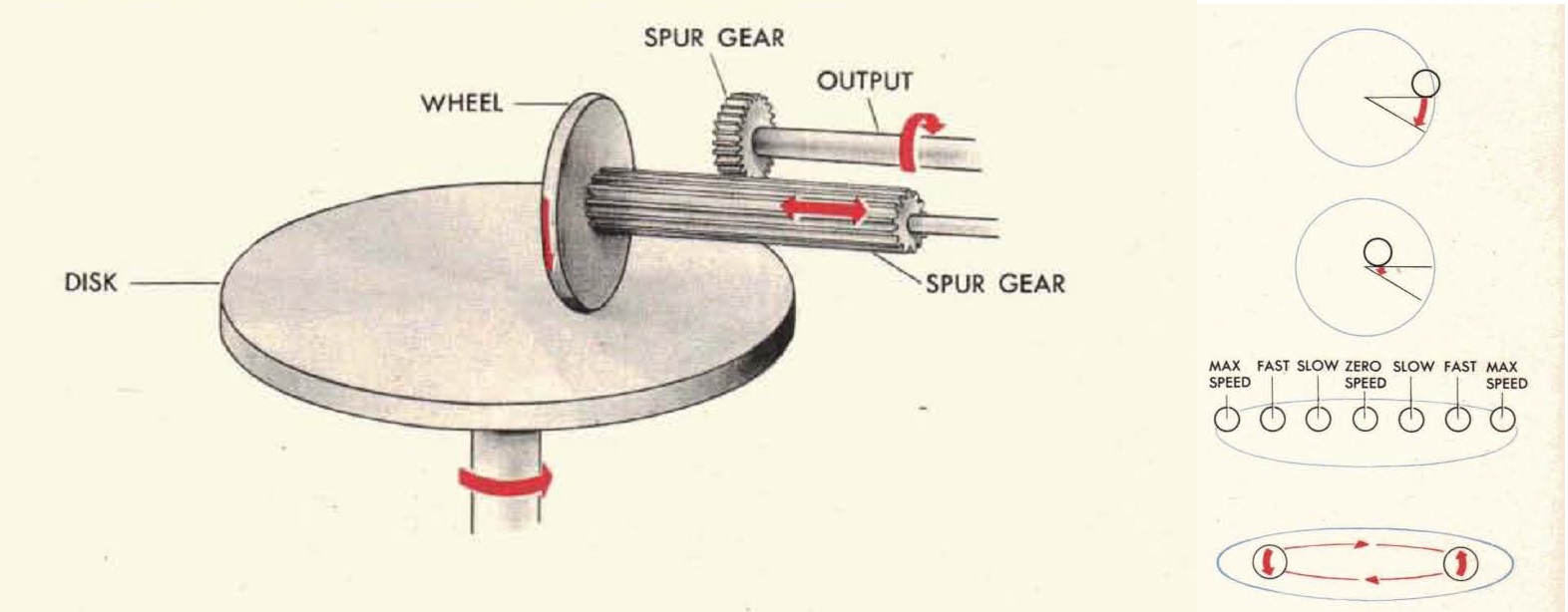
A Disc Integrator
The basic theory behind the Vickers Clock was to provide a mechanism for taking a starting range at a given time, and then applying a range rate set by the operator to it. It did this using a variable-speed drive called a disc-and-roller integrator.4 This was composed of a disc spun at a constant speed by a clockwork mechanism, which drove a roller that could be moved across the disc. The roller was attached to a rod that drove the clock's pointer. If the roller was close to the center of the disc, it would spin slowly, while it would spin quickly towards the rim. This basic principle would be used in virtually all mechanical fire-control systems. Because the Vickers Clock had been developed before it was realized that ships on constant courses do not necessarily have a constant range rate, it was difficult to change the range rate while it was running, and doing so could damage the disc. However, it did have a handle to rotate the face of the clock, allowing corrections to be made based on spotting, and several different scales could be chosen depending on the range of the engagement. On the whole, it was a significant advance in gunnery technology, and most navies quickly fitted all of their ships with similar devices.
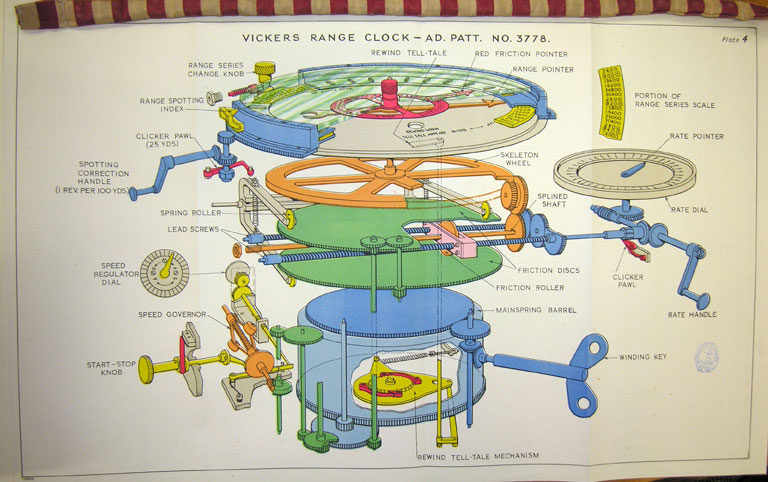
A Vickers Clock
While the Dumaresq and the Vickers Clock marked a significant advance in the technology of fire control, there was still more work to be done. They relied very heavily on their operators, who might be poorly-trained or distracted by the heat of battle, and neither was good at handling situations in which either ship involved was maneuvering.
Next time, we'll discuss the two men who developed the next generation of systems for the Royal Navy, systems that the RN would take to war against the High Seas Fleet.
1 There are often errors in rangefinder output, and various means of mitigating these errors were devised. However, these are subjects I'll have to come back to later. ⇑
2 A large proportion of my readers are probably saying "well, duh", and wondering why they didn't figure this out immediately. I'll agree that this is the sort of thing you should be able to figure out after a few weeks of vector-based physics, and it initially confused me. It appears that the modern concept of a vector was only developed around 1880, which is surprisingly late, and took a while to reach the attention of naval officers. To those who don't think in math, it's probably not obvious at all, and I can only apologize for this digression. ⇑
3 Target course and speed had to be guessed, but these could be estimated with a reasonable degree of accuracy by an experienced observer. ⇑
4 For those of you who remember calculus, yes, this device does indeed take the integral of the range rate. Specifically, the number of revolutions of the output shaft is equal to the change in range. ⇑

Comments
With regards to footnote 2, I think it's a safe bet that they didn't figure it out immediately because vectors were still a relatively new, cutting-edge idea at the time these men were being educated.
Interesting. For some reason, I assumed that the concept of vectors dated back to the early days of modern physics, when it actually appears to have not made it into the modern form until about 1880. And it probably took another few decades to make it to Dartmouth.
The period running from the late 19th Century to the middle of the 20th was in general a time when things could go from "we don't even have the mathematics to adequately describe this concept" to fully operationalized, mass-produced technology in the span of a single individual's working life.
I find this dubious.
Matrices and eigenvalues were both developed well before the 1880s.
Though I could see it being like calculus or set theory, where the practical utility came first and the rigorous theoretical underpinnings second.
But nautical matters tend to involve more practical utility than they do deriving things from first principles.
Based on what I can tell from a quick read of wiki, vectors as we understand them today were a 3D simplification of quaternions, developed in the second half of the 1880s. But I'm not a math historian, and any time I see quaternions, my brain just locks up. I'd guess that related concepts were played with by mathematicians for a century or two before, but that doesn't mean they were suitable for general consumption, in the same way that Principia is a lot harder to understand than a Calc I textbook.
@Lambert
In this case it was as you suggest with the first part of your statement: the theory came first followed by the practice. Dynamics was quite mature by the time in question, including of course the understanding that motion could be deconstructed into its components.
However, vectors as we know them today did not come into widespread use until the closing decade(s) of the 19th Century, and were unlikely to have been included in the education of anyone not working in a field directly related to physics or mathematics, hence why it's unlikely that a naval officer of the period would automatically think about dynamics in vector terms.
In the more general sense, of thinking about the decomposability of the motion of the ships, that kind of knowledge of dynamics just wasn't very useful to seamen before unrelated technological changes ushered in the age of long-range gunnery. I don't know for sure, but I doubt much rigorous knowledge of mechanics would have made it into their training or education.
It's also worth keeping in mind that this was a time when many fields of endeavor which had previously relied on a judicious marriage of traditional rules-of-thumb with personal experience and intuition were first being subjected to extensive mathematical and scientific analysis. You can get a surprisingly long way with the old, "un-scientific" ways, something we often forget, but which is apparent if you study, for instance, the pre-modern history of Naval Architecture.
So were all the systems exchanging data via human voice at this point? The rangefinder operator called out ranges to the rangekeeper operator and the rangekeeper operator called out solutions to the gun operators?
Also, when you say the Dumaresque's solution was 'checked against reports coming in', are these new range/bearing/speed reports, or did it also accept spotter reports?
That's actually something I'm planning to write up as a separate post. By this point, voice transmission from the transmitting station to the guns wasn't really practical, even with voice tubes, and electrical range transmission started around 1900. But it was kind of cantankerous, and you still needed men in the loop to make it work.
Both, and spotting was often the most important source of data. If you have the target straddled (shells falling on both the near and far sides) and then your salvos start falling short or long instead, it means that you need to adjust both the range and the range rate. And the later means adjusting your synthetic solution.
Wouldn't sea navigation have involved thinking about vectors when computing courses with drift?
That's probably how we'd analyze it today, but you could do it without understanding vectors. You're on course X, made so much distance good, and had so much leeway at right angles to course X.